2.2.2. Compara fracciones reduciendo a común denominador y obtiene fracciones equivalentes.

Reducir fracciones a común denominador es encontrar otras fracciones equivalentes a las originales, de forma que tengan todas igual denominador.

 Ejercicio 1)   ¿Cómo se hace?  Pasos:

1) Calculamos el mínimo común múltiplo de los denominadores

 2) Como denominador de las nuevas fracciones ponemos el mcm calculado antes.

 3) Como numerador de cada nueva fracción, ponemos el resultado de dividir el mcm entre el denominador y multiplicar por el numerador.

Ejemplo: Reducir a común denominador las fracciones

 1) 

 2) 

 3) 

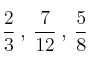
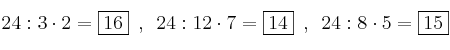
El resultado sería:

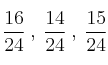
Ejercicio 2)      Ahora  COMPARA las fracciones.

...

Rúbrica  (1punto cada aspecto)

1. Sabe sacar factores.

2. Halla correctamente  el m.c.m

3.Presenta bien la factorización y el termino matemático de m.c.m.

4.Pone como denominador de todas las fracciones  el m.c.m.

5.Calcula bien los numeradores.

6. Se organiza bien en el papel.

7. Reconoce con el signo igual la equivalencia de las distintas fracciones.

8. Compara las fracciones con igual denominador.

9. Compara las fracciones equivalentes a las halladas.